Mathematical modeling to mitigate the effects of COVID-19 in the tourism sector in Peru
Esta obra está bajo licencia internacional Creative Commons Reconocimiento 4.0
Recibido: 30/08/2020 Revisado: 05/09/2020 Aceptado: 10/09/2020 Publicado: 25/10/2020
Palabras clave: COVID-19, turismo, modelación matemática, toma de decisiones.
ABSTRACT
Based on the need to make accurate decisions in the face of the COVID-19 pandemic in Peru, pandemic in Peru, specifically for the recovery of the tourism sector. For this purpose, a characterization of the behavior of the pandemic was carried out in the first three months of its development, based on the analysis of trends and the determination of the effective reproduction number (Rt) from statistical-mathematical methods. A variant of the SIR mathematical model was applied to forecast the possible evolution of the pandemic. This model was adjusted with the GlobalSearch optimization strategy of the MATLAB software. His solution used the MATLAB function ode23tb, which uses a combined Runge-Kutta algorithm with a trapezoidal rule algorithm. With the application of the Kaizen strategy as a means of continuous improvement, a set of actions were proposed that could be carried out today and that would allow the recovery of the tourism sector to be faced in a better situation. The behavior of the Rt and the simulation carried out showed that the mitigation measures established are insufficient to substantially reduce the impact of the pandemic, predicting that, by the end of 2020, the number of infected could reach the figure of 840 thousand and the deaths would exceed the 44 thousand.
INTRODUCCIÓN
La pandemia de la COVID-19 ha infectado a más de 25 millones de persona en todo el mundo y ha provocado la muerte, hasta el momento, de más de 857 mil eres humanos. Estas estadísticas serán muy superiores en los próximos meses y las cifras se incrementarán de manera preocupante en muchas regiones del planeta. El impacto no tendrá solamente un carácter social y de salud, sino que tendrá un fuerte impacto económico en todos los continentes, agudizado por la pobreza, el subdesarrollo y la globalización internacionales.
Uno de los sectores de la economía que mayor afectación directa ha tenido es el turismo, determinado por la limitación de circulación de personas que necesariamente impone la pandemia. Antes del inicio de la COVID-19, el turismo representaba más del 10 % del producto interno bruto (PIB) mundial y generaba empleo para el 20 % de la población activa del mundo (Bauzá y Melgosa 2020). Durante el último quinquenio la tendencia del turismo a nivel global fue de un rápido crecimiento y desarrollo. Las llegadas de turistas internacionales crecieron en el último quinquenio un promedio de un 5 % anual hasta alcanzar en el 2019 la cota de los 1 461 millones, lo que equivale a que los ingresos por exportaciones generados por el turismo aumentaron hasta los 1,7 billones de dólares estadounidenses (UNWTO 2019).
Debido a los embates de la pandemia, se espera, según una investigación realizada por el Consejo Mundial de Viaje y Turismo (WTTC por sus siglas en inglés) que se pierdan entre 98,2 y 197,5 millones de empleos en este sector a nivel mundial, con una reducción del PIB global, entre el 30 y el 62 % respecto al año 2019 ((WTTC) 2020). Cualquiera de los escenarios que prevé esta investigación resultarían catastróficos para gran parte de la población mundial, especialmente para los países subdesarrollados.
Entre los años 2015-2018, el crecimiento del turismo en Perú fue muy importante, tanto en número de arribos como en ingresos financieros (UNWTO 2019). Este sector ha cobrado importancia en la economía peruana y hoy representa cerca del 9 % del PIB de país (CEPAL 2020), sin embargo, este ha sido uno de los países más afectados por la Pandemia en América Latina. Al cierre del mes de agosto del 2020 Perú se mantenía como el tercer país más afectado en América y el quinto del mundo, con más de 652 mil casos confirmados y más 28 mil fallecidos (OMS 2020), lo que implica que ya ocurran afectaciones económicas importantes en el país. Según estimó el presidente de la Cámara Nacional de Turismo Carlos Canales, solamente por conceptos de cancelaciones de turistas procedentes de China, Europa, Estados Unidos, Canadá, Francia y Alemania estas pérdidas financieras podrían estar cercanas a los 170 millones de dólares (Delgado 2020). En el mes de marzo de este año 2020, la economía peruana experimentó una caída de 19 %, su peor resultado en treinta años, a raíz de la pandemia de la COVID 19. Esta disminución, sumada a la suspensión de actividades de casi todos los sectores, tendrá un impacto muy negativo en el mercado laboral.
La importancia del turismo en la economía peruana, unido a la baja de los precios de bienes primarios, fundamentalmente de los minerales que exporta Perú, y a la caída de la actividad de China, Europa y Estados unidos como principales socios comerciales, auguran un decrecimiento del país para el año 2020 entre el 4 % y el 4,7 % (Blanco 2020, CEPAL 2020, LCRCE 2020). Esta reducción del PIB dependerá en gran medida del tiempo que perdure la pandemia y de las políticas que se tracen para minimizar sus efectos.
Para la definición de políticas y toma de decisiones en caso de pandemias se requiere de información lo más confiable posible sobre el posible comportamiento de la enfermedad. El uso de modelos físico-matemáticos para predecir este comportamiento ha sido ampliamente extendido en el caso de la COVID-19 (Ndaïrou y col. 2020, Read y col. 2020, Roda y col. 2020, Tang y col. 2020). Estos modelos pudieran ser muy útiles para la planificación de acciones a desarrollar en el sector turístico peruano. En este sentido, resulta especialmente importante para la toma de decisiones, el pronóstico sobre el comportamiento de la epidemia a mediano y largo plazo, sobre todo en la identificación del momento o periodo de tiempo en el que se tendrá la máxima cantidad de infectados. Esta es una cuestión vital para planificar y organizar la cantidad de recursos materiales, humanos y financieros que se requiere en las distintas etapas para que esta situación no rebase las posibilidades locales existentes en el combate de la terrible secuela de muertes que esto ocasiona y a su vez el grave impacto en la economía.
Poder predecir la máxima cantidad de personas infectadas y el periodo en que esto ocurrirá, es de relevante importancia, no solo para asegurar la disponibilidad de recursos materiales y humanos necesarios para combatir la enfermedad, sino porque constituye un momento relevante de referencia para las actividades de planificación relativas a la recuperación económica. Los resultados de la modelación pudieran ser utilizados para atenuar el impacto de la pandemia y para las proyecciones a ejecutar luego de pasado el momento o periodo más crítico.
Otro elemento de relevante importancia en el estudio de epidemias tiene que ver con el comportamiento reproductivo, que es medido a través del número de reproducción efectivo. Este se define como el número medio de infecciones secundarias que provoca un individuo infectado (Cauchemez y col. 2019). El cálculo de Rt puede ser muy útil para determinar la efectividad de las medidas de control en el combate a la pandemia y la organización del servicio en todos los sectores, particularmente en entidades de turismo y recreación. Un Rt >1 significa que la epidemia se propagará, por el contrario, cuando el valor de Rt se mantiene por debajo de uno, la epidemia se extinguirá (Cauchemez y col. 2019). Mientras exista un alto nivel de susceptibilidad inmunológica dentro de una población dada, para mantener a Rt por debajo de uno se requerirá del mantenimiento de medidas de control estrictas como el aislamiento y las restricciones de movilidad. Para determinar el valor de Rt se han desarrollado algunos métodos estadístico-matemáticos (Cori y col. 2013, Wallinga y Teunis 2004).
Entre los modelos más utilizados para describir el comportamiento de una epidemia está el llamado modelo SIR, concebido y publicado por Kermack y McKendrick (1927). Desde el punto de vista físico, es un modelo de compartimientos y cada uno de ellos representa el estado de una población dada (Susceptibles, Infectados, Recuperados). Desde el punto de vista matemático, el modelo está conformado por un sistema de ecuaciones diferenciales ordinarias y su solución permite determinar las cantidades de una población con un status epidémico dado en cada instante de tiempo (Chowell 2017). Para enfermedades nuevas como la COVID-19, toda la población de un determinado país es considerada como susceptible al inicio de la epidemia. El incremento de los casos de infestados dependerá de que se pongan en contacto individuos infestados (I) y sanos susceptibles (S). El número de estos y la contagiosidad del agente infeccioso determinarán la aparición de nuevos casos de infestados.
En el marco de la situación de crisis creada por la pandemia, la toma de decisiones constituye un reto para transformar la realidad y convertir el riesgo en una oportunidad. Por su carácter simple y preciso el pictograma chino que expresa ese concepto 与机遇, está integrado por dos caracteres RIESGO y OPORTUNIDAD (González de Rivera 2001).
En este trabajo se realizó, a partir del análisis de los datos históricos y de la determinación del número de reproducción efectivo, una caracterización del comportamiento de la epidemia de la COVID-19 en Perú. También se aplicó el modelo SIR para la pandemia de la COVID-19 en el país. Con los resultados de las simulaciones realizadas a partir del uso del modelo, la determinación del número de reproducción efectivo de la pandemia y la aplicación de la estrategia Kaizen como vía para la mejora continua, se proponen acciones para aprovechar el período de bajo o nulo número de turistas, con vistas a ser más eficiente y competitivos ante la nueva normalidad.
MATERIALES Y MÉTODOS
Caracterización del comportamiento de la pandemia en Perú
Para la caracterización del comportamiento de la pandemia en Perú se emplearon los datos del reporte diario de la OMS (2020). Estos datos incluyeron el número de contagiados acumulados en el país, así como el número de recuperados y fallecidos en el período comprendido entre el día 6 de marzo y el 31 de julio del 2020. La cantidad de infectados activos se determinó de forma diaria como la diferencia entre los infectados acumulados y los fallecidos y recuperados acumulados.
El comportamiento de la cantidad de estos grupos poblacionales fue graficado a través del tiempo y se realizó un análisis de tendencia apoyado en el comportamiento del número de reproducción efectivo de la epidemia. Este último, para el mismo periodo de tiempo, se determinó utilizando el método estadístico-matemático de Cori y col. (2013). Los datos para la determinación de Rt para los casos de Lima y El Cusco (Segovia, 2020).
Aplicación del modelo SIR
El modelo SIR, siendo un modelo de compartimientos, se representó físicamente como en la figura 1. Cada recuadro representa el número de personas de un grupo poblacional según sea, (S) para el grupo de los susceptibles de contagio, (I) para el grupo de los infectados y (R) para el grupo de los recuperados. Para esos tres grupos poblacionales es la representación más elemental del modelo SIR. La aplicación del modelo SIR para el caso de Perú se realizó añadiendo el compartimiento de los fallecidos (F) reconocido por (Brauer, Castillo-Chavez, y Feng 2019, Getz y col. 2018, Ndaïrou y col. 2020).
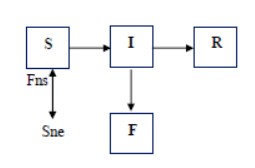
También se utilizó la variable (Sne) como el número de susceptibles no expuestos y (Fns), definido por Sánchez y col. (2020), como el flujo medio neto de personas que transita entre los compartimientos de susceptibles expuestos (S) y el de susceptibles no expuestos (Sne). El Fns será positivo en el caso que el número de personas que entren al compartimiento S sea mayor que las que salen de dicho compartimiento y será negativo en caso contrario. La suma de todos los grupos poblacionales representa la población total considerada en el estudio (N), siendo de 32 162 184 personas para el caso de Perú (INEI 2020).
N=Sne+S+I+R+F (1)
Para la deducción del modelo matemático y teniendo en cuenta las características de la pandemia, se realizaron las siguientes consideraciones:
1.El desenlace de la enfermedad es la muerte o la inmunidad completa, o sea, los infectados se convertirán en recuperados (R) o en fallecidos (F).
2.Existe una mezcla homogénea de infectados y susceptibles expuestos, por lo que toda la población expuesta tiene la misma probabilidad de ser.
3.La tasa de contagio es proporcional al número de infectados.
4.La velocidad de nuevos contagios es proporcional al número de infectados (I) y de susceptibles expuestos (S) que se pongan en contacto.
5.La población total es contante y el sistema es cerrado, o sea, no se tienen en cuenta los nacimientos, las muertes por otras causas, ni las migraciones.
El modelo matemático se obtiene partir de la aplicación general del balance de masa aplicado a cada grupo poblacional, que se representa por la siguiente ecuación:

Al aplicar este balance de masa general a cada grupo poblacional se obtiene el siguiente sistema de ecuaciones diferenciales ordinarias:
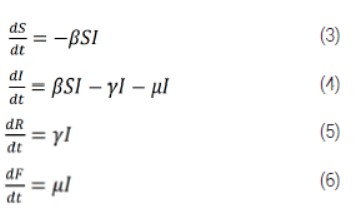
Donde:
- Cada se define como la velocidad de acumulación de una población en un compartimiento dado.
- β,γ,y,μ son las velocidades específicas de infestación, recuperación y muerte. También constituyen parámetros del modelo matemático.
También fueron considerados el número inicial de susceptibles expuestos (S0) y Fns como parámetros a los efectos del ajuste del modelo.
Con el ajuste del modelo se determinaron los parámetros del mismo a partir de la solución de un problema de optimización de mínimo, cuya función objetivo, ecuación 7, es el coeficiente de variación porcentual promedio de los residuos, que constituyen la diferencia entre las predicciones y los datos reales ecuación (Bartholomew-Biggs 2008).
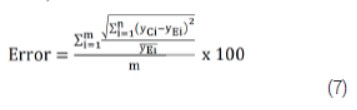
Donde:
•m y n son el número de variables respuesta que se ajustan y el número de puntos experimentales respectivamente.
•yCi son los valores de la variable respuesta calculados con el modelo en el punto experimental “i”
•yEi son los valores reales de la variable respuesta en el punto experimental “i”.
Las variables respuestas son el número de personas en cada uno de los grupos poblacionales.
Para la optimización del ajuste se tomaron como límites de los parámetros:

La solución del sistema de ecuaciones diferenciales que constituye el modelo matemático del sistema se realizó utilizando el método numérico de Runge-Kutta combinado con un método trapezoidal, combinación implícita en la función ode23tb de MATLAB (The MathWorks Inc. 2017). Por esta vía se obtuvieron los valores de las variables que predice el modelo, tanto para el ajuste del mismo, como para las simulaciones realizadas posteriormente. Para el ajuste se utilizó la estrategia de optimización global GlobalSearch de MATLAB, empleando la función fmincon. Los valores reales de las variables respuestas para el ajuste fueron los mismos utilizados para la caracterización.
La estrategia Kaizen como vía para la mejora continua
Con vitas a la recuperación turística ante la nueva normalidad, las acciones que se proponen se basaron en la estrategia Kaizen. El Kaizen Blitz (o bombardeo de mejoras). Masaaki Imai, lo define como: “Mejoramiento y aún más, mejoramiento continuo que involucra a todos, gerente y trabajadores por igual (Suáres, Castillo, y Miguel 2001).
Principios rectores, técnicas y herramientas de la filosofía Kaizen
Se utilizó como principio el método de las 5´S. El objetivo de este método es mantener y mejorar las condiciones de organización, el orden y limpieza, así como las condiciones de trabajo, seguridad, clima laboral, motivación personal y eficiencia. Un concepto que continuamente aplicado a la gestión y administración del puesto de trabajo conduce a un proceso de mejora continua, consiguiendo mejorar la productividad, competitividad y calidad en las empresas. Las cinco S se refieren a:
• SEIRI.- ORGANIZACIÓN. Consiste en identificar y separar los materiales necesarios de los innecesarios y desprenderse de estos últimos.
• SEITON.- ORDEN. Se trata de establecer el modo en que deben ubicarse e identificarse los materiales necesarios, de manera que sea fácil y rápido encontrarlos, utilizarlos y reponerlos.
• SEISO.- LIMPIEZA. Basada en identificar y eliminar las fuentes de suciedad, asegurando que todos los medios se encuentran siempre en perfecto estado, en las condiciones actuales, este elemento es altamente valorado en las instalaciones turísticas.
• SEIKETSU.- CONTROL VISUAL. El objetivo es distinguir fácilmente una situación normal de otra anormal, mediante normas sencillas y visibles para todos.
• SHITSUKE.- DISCIPLINA Y HÁBITO. Consiste en trabajar permanentemente de acuerdo con las normas establecidas.
La mejora continua tiene como requisito fundamental el establecimiento de estándares. El Ciclo PDCA, son el acrónimo de las palabras inglesas Plan, Do, Check, Act, equivalentes en español a Planificar, Hacer, Verificar, y Actuar. Constituye una estrategia de mejora continua de la calidad.
El turismo es un sistema cuya operación está integrada por diferentes procesos que constituyen un conjunto indisoluble, estos son: el viaje, el alojamiento, la alimentación y la recreación del viajero. Según la Organización Mundial del Turismo (UNWTO 2013), turismo son aquellas “Actividades que realizan las personas durante sus viajes y estancias en lugares distintos al de su entorno habitual, por un período de tiempo consecutivo inferior a un año con fines de ocio, por negocios u otros motivos”.
Uno de los principios rectores del Kaizen turístico es el rediseño de los procesos, y en las actuales condiciones, que es momento de reinventar lo que se hace para que responda a las nuevas necesidades de los clientes a la nueva realidad, este rediseño cobra relevante importancia.
La aplicación del Kaizen requiere de métodos sistemáticos y participativos, entre los utilizados con éxito está el TKJ (Team Kawakita Jiro), consiste en transformar al grupo de trabajo en un equipo, en la situación actual. Es preferible, para la gerencia y los trabajadores, la lucha por un objetivo común, que es salvar y hacer crecer el negocio para conservar el trabajo, en vez de soluciones individuales, que no generar sinergia. Para el desarrollo de este método se utilizaron las fases propuestas por Valles (2015), que se relacionan:
•Sensibilización/Integración. Crear un clima de auto confianza, participación y espíritu de equipo.
•Construcción de hechos. Análisis de la situación, determinación de problemas y posibles soluciones, identificar los obstáculos subjetivos y como accionar para su erradicación.
•Compromisos. Cada miembro del equipo se concientiza de la situación, y sabe que debe hacer para aplicar las soluciones.
•Seguimiento. Se revisan las acciones que facilitan el cambio y se elimina o reduce aquello que supone un obstáculo. Control y corrección para lograr las soluciones.
RESULTADOS Y DISCUSIÓN
En la figura 2 se muestra el comportamiento del número de infectados por la pandemia en Perú. La curva de color carmelita representa el número de infectados por la pandemia que se acumulan a través del tiempo y la de color azul se refiere a la cantidad de infectados que existen en una fecha dada, que se han denominados infectados activos. Se observa claramente que durante los meses de marzo, abril y mayo la pandemia en el país sigue un crecimiento exponencial, típico de cualquier brote epidémico. Aproximadamente, a partir del 2 de junio, señalado en el gráfico, ocurre un cambio brusco de la tendencia y el incremento de los infectados acumulados toma una tendencia lineal, esto provoca el aplanamiento de la curva de infectados activos e incluso una ligera disminución de estos durante el mes de junio.
El cambio de inflexión experimentado el día 2 de junio se puede interpretar como el resultado del efecto de las medidas de control implementadas durante el mes de mayo por el Ministerio de Salud y la Presidencia de la República, entre otras, en las resoluciones N° 248-2020 (MINSA 2020a), N° 254-2020 (MINSA 2020b), N° 309-2020 (MINSA 2020c), N° 314-2020 (MINSA 2020d) y el decreto presidencial N° 059-2020 (Presidencia de la República 2020)
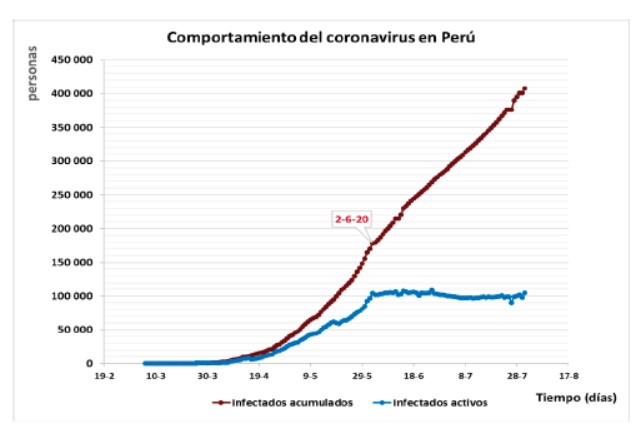
Figura 02: Curvas que representan la tendencia del número de infectados por la pandemia en Perú
A pesar del favorable cambio de
pendiente de la curva de infectados, el comportamiento estacionario, en forma
de meseta, que ha mostrado el número de infectados activos a partir de ese
momento, evidencia que no se ha podido controlar la pandemia en el territorio
nacional y que las medidas implementadas no han sido suficientemente efectivas.
El comportamiento obtenido del número de reproducción efectivo Rt, que
se muestra en la figura 3, es coherente con el anterior análisis. Este
comportamiento devela que el Rt al inicio de la pandemia tenía un
alto valor, indicador del elevado poder de contagio en ese momento. En los
inicios del mes de junio, coincidentemente con el inicio de la meseta en la
curva de infectados activos, el valor de Rt toma un valor muy
cercano a uno y se mantiene cercano a ese valor durante los próximos dos meses.
Este comportamiento del Rt significa que cada infectado provoca solamente,
como promedio, el contagio de un individuo susceptible y, por tanto, teniendo
en cuenta los recuperados y fallecidos, el número de infectados activos se
mantenga aproximadamente constante. Por la razón anterior, el número de
infectados activos se ha mantenido durante dos meses cercano a las 100 000
personas.
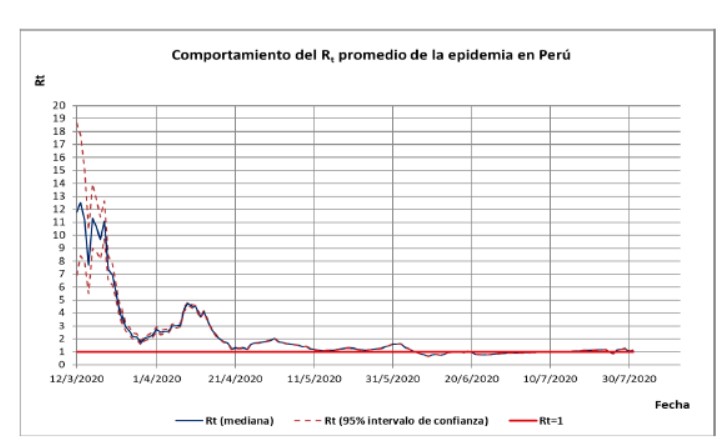
Figura 3. Curva de comportamiento del Rt en Perú.
El análisis realizado ha tenido en
cuenta solamente la situación a nivel de todo de país, aunque un comportamiento
similar se presenta a lo largo de todo el territorio nacional. La capital Lima,
que tiene una población de alrededor de 9,7 millones de habitantes (INEI 2020) y representa cerca del 29,7 % de la población del país, ha presentado
un similar comportamiento con relación al Rt. Un departamento de
mucha menor población como es el caso de El Cusco, de poco más de 1,2 millones
de personas (Segovia,2020), presenta igual comportamiento del Rt. El
mantenimiento del valor de Rt en el entorno de uno para cada uno de
estos casos corrobora que las medidas de mitigación establecidas no tienen la
eficacia suficiente para extinguir la pandemia. En la figura 4 se muestra el
comportamiento del valor de Rt para los departamentos de Lima y El Cusco.
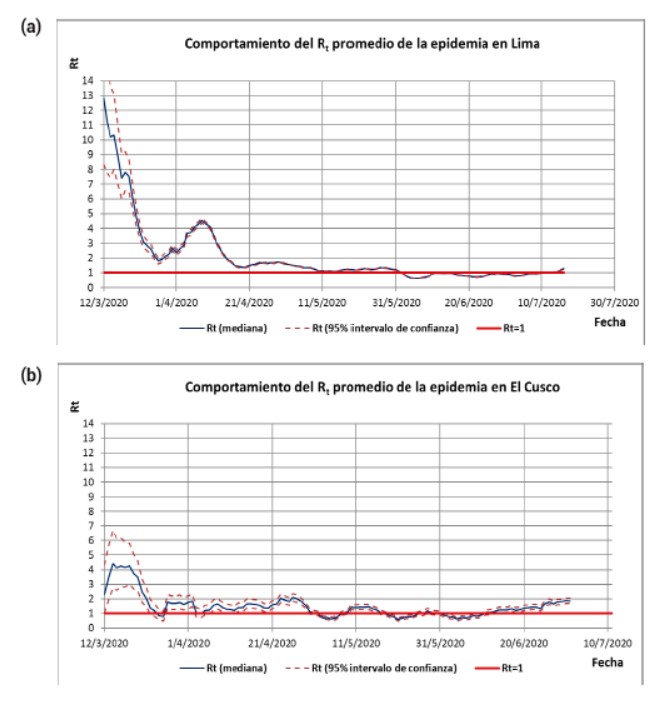
Figura 4. Curvas de comportamiento del Rt en Lima (a) y El Cusco (b)
Es importante señalar que, aunque se logre reducir el Rt por debajo de uno, la extinción de la pandemia se lograría solamente con el mantenimiento de las medidas de mitigación. Esto solo se lograría en un periodo de tiempo significativamente grande y sería un resultado muy poco sostenible. La flexibilización de las medidas de control, combinado con la presencia de algunos pocos casos de infectados en el territorio nacional, dispararía nuevamente el crecimiento de la pandemia. Estos comportamientos de rebrotes ya han sido observados en algunos países.
Teniendo en cuenta el comportamiento de la pandemia de la COVID en Perú, caracterizada por un cambio de tendencia a partir del día 2 de junio, la aplicación del modelo SIR se realiza para los periodos antes y después de la referida fecha. Esta diferencia de tendencia está altamente determinada por el comportamiento de la población y las medidas de control establecidas por las autoridades. La diferencia de este comportamiento no permite un único ajuste del modelo para ambas zonas ya que el valor de los parámetros del modelo tomaría valores significativamente diferentes entre ambos casos. El ajuste del modelo para el primer periodo carece de importancia a los efectos de los pronósticos, por tal razón, los datos empleados para dicho ajuste se tomaron entre los días 2 de junio y 31 de julio. Los valores de los parámetros determinados durante el ajuste del modelo se muestran en la tabla 1.
Tabla 1. Parámetros del modelo cinético estimados.

Empleando en el modelo los parámetros presentados en la tabla 1 se realiza la simulación del comportamiento de la pandemia a partir del 31 de julio hasta finales de este año 2020. Los resultados de la simulación se muestran en la figura 5. Esta figura integra el comportamiento real de la pandemia hasta el 31 de julio (con marcadores circulares) con el comportamiento pronosticado por el modelo SIR hasta el 31 de diciembre (con líneas continuas).
Como resultado de la simulación, como se observa en la figura, la cifra de infectados acumulados de la pandemia pudiera sobrepasar las 843 mil personas el 31 de diciembre y los fallecidos pudieran ser más de 44 500. También se observa que el comportamiento de los infectados activos mantiene una tendencia prácticamente en forma de meseta casi hasta el mes de noviembre y el número de estos se mantendrá entre 50 mil y 100 mil hasta finales de año. Este último elemento mantendrá la congestión del sistema de salud en el país y la complejidad de todo el sistema logístico necesario para combatir la pandemia.
La simulación realizada se corresponde con el ajuste del modelo y los datos procesados correspondientes al periodo entre el día 2 de junio y el 31 de julio, por lo que el pronóstico estará determinado matemáticamente por el valor de los parámetros que se calcularon durante dicho ajuste y que a su vez dependen de las condiciones existentes en ese periodo y de las medidas de control y mitigación de la pandemia que la condicionan. La anterior reflexión significa que la evolución de la pandemia pudiera diferir sustancialmente de la anteriormente presentada si se decide flexibilizar las medidas de control de forma anticipada. Se pudiera llegar a un comportamiento similar al que se estaba dando antes del 2 junio, con un crecimiento exponencial del número de infectados y una curva de infectados activos que tomaría una forma de pico y que pudiera alcanzar en pocos días una cifra de cerca de 200 mil personas.
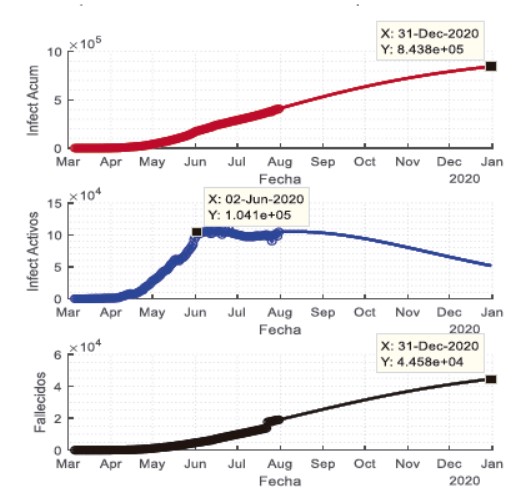
Figura
5. Pronóstico de comportamiento de los infectados y
fallecidos por la pandemia en Perú.
Teniendo en cuenta los resultados de la caracterización realizada sobre el comportamiento de la pandemia de la COVID-19 en Perú y los resultados de la simulación que se obtienen a partir de la aplicación del modelo SIR, se infiere que la situación del país en la coyuntura actual es muy compleja y peligrosa. La efectividad de las medidas de control y mitigación de los efectos de la pandemia son muy poco consistentes y se pudiera entrar en una etapa de un mayor crecimiento del número de infectados que agravaría la situación. El ejemplo de varias regiones del mundo en las que se flexibilizaron anticipadamente las medidas de control evidencia esta afirmación.
Se está combatiendo un virus de alta capacidad de contagio y una letalidad nada despreciable. Para que ocurra una reducción significativa del número de nuevos infectados y haya una tendencia a la extinción de la pandemia, el valor de Rt debe permanecer por debajo de uno. Esto es lograble con estrictas medidas de control o con la reducción significativa del número de personas susceptibles, que se pudiera lograr con la aplicación de una vacuna que aún no está disponible para la población mundial, aunque algunos candidatos vacunales ya están en fases avanzadas de ensayos clínicos y son la gran esperanza en el momento que vive la humanidad.
Ante la situación descrita, no es recomendable la apertura de muchos sectores de la economía y especialmente el turismo, que es de gran importancia en el contexto peruano, debería aplazar su reapertura hasta que cambie significativamente la coyuntura actual.
Sería más aconsejable y sensato centrar los esfuerzos en la preparación para afrontar la nueva normalidad que se establecerá después de vencida la pandemia o al menos en condiciones de menos severidad que la actual.
Un factor positivo que nos ayudaría a mejorar, es el hecho de que no se registra una destrucción de capital (infraestructura, recursos y capital humano), como lo que ocurre en otros desastres, guerra y terremotos, sin embargo, es importante evitar quiebras bancarias, ya que generarían una depresión o una recesión continua, como la registrada en 1929.
A continuación, se proponen un conjunto de acciones para aprovechar este tiempo sin turistas o con cantidades mínimas, y estar adaptados, ser más competitivos, en la nueva normalidad.
I. Diagnóstico turístico.
El diagnóstico turístico es la etapa donde se establece y evalúa la situación de un destino en un momento determinado, es un corte en el tiempo, un balance de recursos y servicios turísticos como elementos básicos de la oferta turística, mediante el mismo deben identificarse las brechas, para alcanzar los objetivos. Su éxito depende de la selección y calidad de la información utilizada.
1. Revisar las páginas Web y/o encuestas donde se realizan comentarios sobre la instalación, precisando las quejas reiteradas.
2. Fidelización del cliente.
3. Tendencia de la demanda
4. Estudio de los atractivos del lugar y variedad de la oferta.
5. Situación de la infraestructura.
6. Preparación del personal para enfrentar los nuevos requerimientos de los servicios: calidad e inocuidad de los alimentos, limpieza a fondo de los locales, condiciones higiénicas.
7. Relación con la Comunidad.
8. Situación de la seguridad y la atención médica en la localidad, cuestiones altamente valoradas en la nueva normalidad.
II. Propuesta de solución de los problemas identificados.
La solución de los problemas detectados en el diagnóstico, requieren de un proceso estratégico, conducentes al logro de los objetivos trazados, algunas cuestiones dependerán de inversiones y debe pensarse cuidadosamente en el presupuesto requerido, sobre todo en las difíciles condiciones actuales, pero es sorprendente que las buenas prácticas y el trabajo con calidad, no solo fideliza al cliente, e incrementa los ingresos, disminuye los costos, porque las cosas salen bien a la primera, y no siempre requieren inversión.
En la nueva realidad, el único camino que tienen las empresas para seguir compitiendo, es la continua implementación de las mejores prácticas, principios, estrategias y tecnologías de gestión, para dar solución a los problemas y elevar su competitividad. En este entorno de crisis es el momento de pensar en tipo de estrategias como el Kaizen (Mejora Continua). Con la aplicación de esta estrategia se lograría:
1.Incrementar el rendimiento de unos trabajadores más motivados, gracias a la formación y el ambiente de trabajo favorable.
2. Eliminar el desperdicio, mejor aprovechamiento de los recursos, disminuyendo los costos.
3. Creación de nuevos productos y servicios acordes a las nuevas necesidades de los clientes
4. Aumentar el nivel de calidad de los productos o servicios, contando con unos talentos más productivos en la empresa.
5.Mejorar la satisfacción de los clientes, quienes obtendrán un mejor servicio y/o productos.
Aunque la estrategia Kaizen conlleva al establecimiento de ciclos, como todo proceso de mejora continua, seguidamente se muestra en el diagrama Gantt de la figura 6 el conjunto de actividades que se proponen a desarrollar en el primer ciclo del proceso de mejora para el caso de la recuperación y reanimación del sector turístico en Perú. Este diagrama ha sido confeccionado tomando en cuenta los aspectos relacionados con el diagnóstico y los principios generales del trabajo en equipo que precisa el método TKJ.
Aunque el tiempo de duración de las actividades dependerá de las condiciones técnico-organizativas de cada entidad y el momento de inicio del proceso global será decidido previamente por los directivos, de manera ilustrativa, en el diagrama propuesto se fija como fecha de inicio del proceso el día primero de octubre y los tiempos de cada actividad se han establecido a partir de la experiencia de los autores.
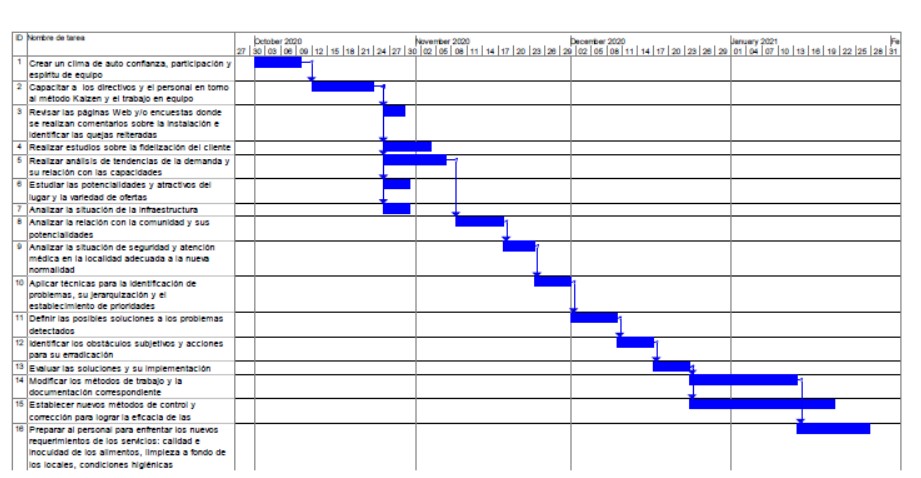
Figura 6. Gantt de planificación de actividades propuestas para el proceso de recuperación del sector turístico en Perú.
En el diagrama se observa que algunas actividades comienzan simultáneamente. Esto se pudiera realizar cuando no existen interdependencia entre estas y cuando se cuenta con suficiente personal para llevarlas a cabo de manera independiente. De esta forma se reduce el tiempo del proceso global y en ocasiones se requerirá de algunas actividades extras para integrar los resultados.
CONCLUSIONES
La caracterización sobre el comportamiento de la pandemia en Perú demuestra que, luego de un inicio con un crecimiento exponencial del número de infectados, se ha logrado un cierto aplanamiento de la curva de infectados activos dada la eficacia de las medidas gubernamentales de control que se establecieron en el mes de mayo. Aunque estas han logrado un efecto positivo, son insuficientes en el sentido de establecer condiciones de normalidad, algo evidenciado por el comportamiento del número de reproducción efectivo en un valor cercano a uno. Esta caracterización y los resultados del pronóstico a partir de la aplicación del modelo SIR indican, que, en las condiciones actuales, determinadas por las medidas y el modo de hacer las cosas, el número de infectados seguirá creciendo y la situación epidemiológica será muy compleja para finales de año, por lo que no será recomendable flexibilizar las medidas actuales, sino por el contrario, se precisa de medidas más severas para detener el contagio. Ante esta situación, la apertura de la actividad turística no es recomendable, siendo más prudente preparar al sector para periodos posteriores a la pandemia. La aplicación de la estrategia Kaizen podría ser un elemento clave de la recuperación.
REFERENCIAS BIBLIOGRÁFICAS
- (WTTC), World Travel and Tourism Council. (2020). Travel & tourism recovery scenarios 2020 and economic impact from covid-19.
- Bartholomew-Biggs, M. 2008). Nonlinear Optimization with Engineering Applications. Vol. 19, Optimization and Its Applications. New York, USA: Springer.
- Bauzá, Felio José, y Francisco Javier Melgosa. 2020. “El turismo después de la pandemia global. Análisis, perspectivas y vía de recuperación.” In. España: Asociación Española de Expertos Cietíficos en Turismo.
- Blanco, A. (2020). El profundo, pero transitorio, impacto del COVID-19 en la economía latinoamericana. Real Instituto Elcano.
- Brauer, F., C. Castillo-Chavez, y Z. Feng. (2019). “Mathematical Models in Epidemiology.” In Texts in Applied Mathematics. Princeton University, USA.
- Cauchemez, S., N. Hoze, A. Cousien, B. Nikolay, y Q. Ten Bosch. (2019). “How Modelling Can Enhance the Analysis of Imperfect Epidemic Data.”Trends in Parasitology 35 (5):369-379. doi: 10.1016/j.pt.2019.01.009.
- CEPAL, Comisión Económica para America Latina y el Caribe. (2020). Informe especial COVID-19. Oeganización de Naciones Unidas.
- Chowell, G. 2017. “Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A primer for parameter uncertainty, identifiability, and forecasts.” Infectious Disease Modelling 2 (1):379-398. doi: 10.1016/j.idm.2017.08.001.
- Cori, A., N. M. Ferguson, C. Fraser, y S. Cauchemez. (2013). “A new framework and software to estimate time-varying reproduction numbers during epidemics.” American Journal of Epidemiology 178 (9):1505–1512
- Delgado, J. M. (2020). Turismo y medio ambiente en un escenario post covid-19. In El turismo después de la pandemia globa. Análisis, perspectivas y vías de recuperación. España: Asociación Española de Expertos Cietíficos en Turismo
- Getz, W. M., R. Salter, O. Muellerklein, H. S. Yoon, y K. Tallam.( 2018). “Modeling epidemics: A primer and Numerus Model Builder implementation.” Epidemics 25 (2018):9–19. doi: 10.1016/j.epidem.2018.06.001.
- González de Rivera, J. L.( 2001). “Psicoterapia de la crisis.” Revista de la Asociación Española de Neuropsiquiatría:1-13.
- INEI. (2020). Estado de la población peruana 2020. edited by Fondo de población de las naciones unidas.
- Kermack, W. O., y A. G. McKendrick. (1927). “Contributions to the Mathematical Theory of Epidemics.” Proceedings of the Royal Society of London 115 (772):700-721.
- LCRCE. (2020). La economía en los tiempos del covid-19. Informe semestral de la región America Latina y el Caribe. edited by Banco Mundial.
- MINSA. (2020a). Resolución Ministerial N° 248-2020-MINSA. Recomendaciones para el uso apropiado de mascarillas y respiradores por el personal de salud en el contexto del COVID-19. Lima, Perú: El Peruano.
- MINSA. (2020b). Resolución Ministerial N° 254-2020-MINSA. Manejo de personas afectadas por COVID-19 en áreas de atención crítica. Lima, Perú: El Peruano.
- MINSA. (2020c). Resolución Ministerial N° 309-2020-MINSA. Lineamientos para el fortalecimiento de acciones de respuesta en establecimientos de salud, redes de salud y oferta móvil frente al COVID-19. Lima, Perú: El Peruano.
- MINSA. (2020d). Resolución Ministerial N° 314-2020-MINSA. Directiva sanitaria para la atención de salud en centros de aislamiento temporal y seguimiento de casos de covid-19 en el perú. Lima, Perú: El Peruano.
- Ndaïrou, F., I. Area, J. J. Nieto, y D. F. M. Torres. (2020). “Mathematical Modeling of COVID-19 Transmission Dynamics with a Case Study of Wuhan.” Chaos, Solitons and Fractals (Journal Pre-proof). doi: 10.1016/j.chaos.2020.109846.
- OMS. (2020). “Coronavirus disease (COVID-19), Situation Report – 134.” https://www.who.int.
- Presidencia de la República. (2020). Decreto de urgencia N° 059-2020. Medidas extraordinarias para garantizar el acceso a medicamentos y dispositivos médicos para el tratamiento del coronavirus y reforzar la respuesta sanitaria en el marco del estado de emergencia sanitaria por el covid-19. Lima, Perú: El Peruano.
- Read, J. M., J. R. E. Bridgen, D. A. T. Cummings, A. Ho, y C. P. Jewell. (2020). “Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions.” medRxiv.
- Roda, W. C., M. B. Varughese, D. Han, y M. Y. Li. (2020). “Why is it difficult to accurately predict the COVID-19 epidemic?” Infectious Disease Modelling 5:271-281. doi: 10.1016/j.idm.2020.03.001.
- Sánchez, H. E., L. B. Ramos, P. A. Galindo, y A. Salgado. 2020. “ Modelación físicomatemática para la toma de decisiones frente a la COVID-19 en Cuba.” Retos de la dirección.
- Segovia Juárez , J. L. (2020). Peopledata1.com. Recuperado 26 de junio de 2020, de https://www.datosabiertos.gob.pe/group/datos-abiertos-de-covid-19
- Suáres, M. F., I. Castillo, y J. A. Miguel. (2001). “La aplicación del Kaizen en las organizaciones mexicanas. Un estudio empírico.” Globalización, Competitividad y Gobernabilidad 5 (1):60-74.
- Tang, B., X. Wang, Q. Li, N. L. Bragazzi, S. Tang, y Y. Xiao. (2020). “Estimation of the transmission risk of 2019-nCoV and its implication for public health interventions.” Journal of Clinical Medicine 9 .2020:462.
- Matlab 9.3.0.713579 (R2017b) (Programa de computador). The MathWorks Inc., Natick, MA, USA.
- UNWTO, Organización Mundial del Turismo. (2013). Recomendaciones de la OMT por un turismo accesible para todos. Madrid, España.
- UNWTO, Organización Mundial del Turismo. (2019). Panorama del turismo internacional.
- Wallinga, J., y P. Teunis. (2004). “Different Epidemic Curves for Severe Acute Respiratory Syndrome Reveal Similar Impacts of Control Measures.” American Journal of epidemiology 160 (6):509–516.